Physical Process¶

Introduction¶

The module physicalmassbalance allows the user to model physical processes and perform mass/mole balances. The user can perform mass balance or mole balance as long as units remain consistent.

How to use

It is recommended that the module be imported as from pychemengg.massbalances import physicalmassbalance as pmb.

The following examples demonstrate how the module physicalmassbalance can be used to solve mass/mole balances for physical processes.

Examples¶

Example 1: How to `define a physical process`¶

Example 1. Consider a mass/mole balance has to be performed on a:

distillation column.
mixer

How can these systems be set up?

# EXAMPLE 1
from pychemengg.massbalances import physicalmassbalance as pmb

# Create instance of distillation column.
distillationcolumn = pmb.PhysicalProcess("distillationcolumn")
# On left hand side is the variable to which the
# instance of PhysicalProcess is assigned.
# Here, the variable is named 'distillationcolumn'.
# Internally, the instance is named 'distillationcolumn', which
# is the string provided as argument to PhysicalProcess().
# These two need not be given the same names, but it is
# convenient if they have the same name.
# The instance stores the name of the process in the
# attribute .processname
print(distillationcolumn.processname)
# The following gets printed on screen
'distillationcolumn'

# Create instance of mixer
# Here the name of variable and process are different for
# demonstration purposes.
mixer = pmb.PhysicalProcess("mixer1")
print(mixer.processname)
# The following gets printed on screen
'mixer1'
NOTE: It is better to use same names to prevent errors.

Example 2: How to `attach streams to a process`¶

Example 2. Consider a mass/mole balance has to be performed on a mixer. Define the process and attach four streams with the following data.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=0.2, c2=0.3, c3=0.5
S2	In	10	c1=0.1, c2=0.2, c3=0.7
S3	In	135	c1=0.4, c2=0.1, c3=0.5
S4	Out	unknown	unknown

# EXAMPLE 2
from pychemengg.massbalances import physicalmassbalance as pmb

# Create instance of mixer
mixer1 = pmb.PhysicalProcess("mixer1")

To attach streams use the method ‘attachstreams’

METHOD 1: Attach streams one at time

S1 = mixer1.attachstreams(streamnames=["S1"])
# NOTE: String has to be placed in [   ]
# NOTE: Use the same names for variable and instance name.

# To assign flowrate use .setflow(flowrate) method
S1.setflow(200)

# To assign fractions use .setfractions(list of fractions) method
S1.setfractions([0.2, 0.3, 0.5])

# Attach 2nd stream
S2 = mixer1.attachstreams(streamnames=["S2"])
S2.setflow(10)
S2.setfractions([0.1, 0.2, 0.7])

# Attach 3rd stream
S3 = mixer1.attachstreams(streamnames=["S3"])
S3.setflow(135)
S3.setfractions([0.4, 0.1, 0.5])

# Attach 2nd stream
S4 = mixer1.attachstreams(streamnames=["S4"])
S4.setflow("-F")
S4.setfractions(["x", "x", "x"])

# The mixer can be printed
print(mixer1)

# Output is as follows:
    ================================
    Process streams for MIXER1 are :
    ================================
    Stream = S1; Flowrate = 200.00; Fractions = ['0.2000', '0.3000', '0.5000']; Extra Info = None
    Stream = S2; Flowrate =  10.00; Fractions = ['0.1000', '0.2000', '0.7000']; Extra Info = None
    Stream = S3; Flowrate = 135.00; Fractions = ['0.4000', '0.1000', '0.5000']; Extra Info = None
    Stream = S4; Flowrate =     -F; Fractions = ['  x   ', '  x   ', '  x   ']; Extra Info = None
    --------------------------------
    END

METHOD 2: Attach all streams at same time

streams = ["S1", "S2", "S3", "S4"]
flowrates = [200, 10, 135, "-F"]
fractions = [[0.2, 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, 0.1, 0.5],["x", "x", "x"]]
S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)
# Print the mixer1 process
print(mixer1)

# Output is as follows:
    ================================
    Process streams for MIXER1 are :
    ================================
    Stream = S1; Flowrate = 200.00; Fractions = ['0.2000', '0.3000', '0.5000']; Extra Info = None
    Stream = S2; Flowrate =  10.00; Fractions = ['0.1000', '0.2000', '0.7000']; Extra Info = None
    Stream = S3; Flowrate = 135.00; Fractions = ['0.4000', '0.1000', '0.5000']; Extra Info = None
    Stream = S4; Flowrate =     -F; Fractions = ['  x   ', '  x   ', '  x   ']; Extra Info = None
    --------------------------------
    END

Example 3: How to `name streams attached to a process`¶

Example 3. Consider a mass/mole balance has to be performed on a mixer. Let there be four streams with the following data.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=0.2, c2=0.3, c3=0.5
S2	In	10	c1=0.1, c2=0.2, c3=0.7
S3	In	135	c1=0.4, c2=0.1, c3=0.5
S4	Out	unknown	unknown

# EXAMPLE 3
from pychemengg.massbalances import physicalmassbalance as pmb

# Create instance of mixer
mixer1 = pmb.PhysicalProcess("mixer1")

METHOD 1: Use somename for stream variable

# Here let the stream names be S1, S2, S3, S4
S1 = mixer1.attachstreams(streamnames=["S1"])
# The variable name on LHS allows the user
# to reference the strings in code.
# For example, to set its flow rate
S1.setflow(200)
# Similarly other streams can be named
S1, S3, S4 = mixer1.attachstreams(streamnames=["S2", "S3", "S4"])

Limitation Use of somename (say S1, S2, S3, S4, NaOH, HCl, crude etc) does not allow easy identification of the process to which the stream is attached.

METHOD 2: Use processname.somename for stream variable

# The streamname can be attached to the process name
# using the dot operator. This allows easy identification
# of the process to which a stream is attached
mixer1.S1 = mixer1.attachstreams(streamnames=["S1"])
# Similarly other streams can be named
mixer1.S2, mixer1.S3, mixer1.S4 = mixer1.attachstreams(streamnames=["S2", "S3", "S4"])
# To assign flow rate:
mixer1.S2.setflow(10)

Limitation Use of processname.streamname does not provide a convenient answer to whether the stream is entering or exiting the process.

METHOD 3: Use processname.somename_in/out for stream variable

# The streamname with 'in' or 'out' can be attached to the process name
# using the dot operator. This allows easy identification
# of the process to which a stream is attached and whether the stream
# is entering or exiting the process.
mixer1.S1_in = mixer1.attachstreams(streamnames=["S1_in"])
# Similarly other streams can be named
mixer1.S2_in, mixer1.S3_in, mixer1.S4_out = mixer1.attachstreams(streamnames=["S2_in", "S3_in", "S4_out"])
# To assign flow rate:
mixer1.S2_in.setflow(10)

Example 4: How to `print physical process and streams`¶

Example 4. Consider a mass/mole balance has to be performed on a mixer. Let there be four streams with the following data.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=0.2, c2=0.3, c3=0.5
S2	In	10	c1=0.1, c2=0.2, c3=0.7
S3	In	135	c1=0.4, c2=0.1, c3=0.5
S4	Out	unknown	unknown

Assign the streams and print the mixer and streams.

# EXAMPLE 4
from pychemengg.massbalances import physicalmassbalance as pmb
mixer1 = pmb.PhysicalProcess("mixer1")

streams = ["S1", "S2", "S3", "S4"]
flowrates = [200, 10, 135, "-F"]
fractions = [[0.2, 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, 0.1, 0.5],["x", "x", "x"]]
S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)

To print the mixer ‘process’

print(mixer1)

# OUTPUT is
    ================================
    Process streams for MIXER1 are :
    ================================
    Stream = S1; Flowrate = 200.00; Fractions = ['0.2000', '0.3000', '0.5000']; Extra Info = None
    Stream = S2; Flowrate =  10.00; Fractions = ['0.1000', '0.2000', '0.7000']; Extra Info = None
    Stream = S3; Flowrate = 135.00; Fractions = ['0.4000', '0.1000', '0.5000']; Extra Info = None
    Stream = S4; Flowrate =     -F; Fractions = ['  x   ', '  x   ', '  x   ']; Extra Info = None
    --------------------------------
    END

To print an individual ‘stream’

print(S1)

# OUTPUT is
    Stream: S1
    Attached to the physical process: MIXER1
    flowrate: 200
    fractions: [0.2, 0.3, 0.5]
    extrainfo: None

Example 5: How to `attach stream from one process to another process`¶

Example 5. Consider a stream exiting process1 and it enters process2. The stream is assumed to be already attached to process1. Let the stream from process1 be called ‘S1’, with flowrate=120 kg/s, and mass fractions = [0.2, 0.15, 0.65]. How can it be attached to process2?

To attach the stream use the setequalto() method.

# EXAMPLE 5
from pychemengg.massbalances import physicalmassbalance as pmb
process1 = pmb.PhysicalProcess("process1")
process2 = pmb.PhysicalProcess("process2")
process1.S1_out = process1.attachstreams(streamnames=["process1.S1_out"], flowrates=[-120], fractions =[[0.2, 0.15, 0.65]])
# Note that since S1 is exiting, it has a negative flowrate
process2.S2_in = process2.attachstreams(streamnames=["process2.S2_out"])
# print S1 and S2 to confirm their data
print(process1.S1_out)
# Output is
    Stream: process1.S1_out
    Attached to the physical process: PROCESS1
    flowrate: -120
    fractions: [0.2, 0.15, 0.65]
    extrainfo: None
print(process2.S2_in)
# Output is
    Stream: process2.S2_out
    Attached to the physical process: PROCESS2
    flowrate: Not yet defined
    fractions: ['Not yet defined']
    extrainfo: None

# Now apply setqualto()
process2.S2_in.setequalto(process1.S1_out, flowdirection="+")
# This means S2 will become equal to S1
# Since S2 is entering, it's flow showuld be positive.
# Therefore, flowdirection = "+"
# print S2 to confirm the method was successful
print(process2.S2_in)
# Output is
    Stream: process2.S2_out
    Attached to the physical process: PROCESS2
    flowrate: 120
    fractions: [0.2, 0.15, 0.65]
    extrainfo: None

Example 6: How to `add or subtract streams`¶

Example 6. Consider streams that enters a mixer.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=0.2, c2=0.3, c3=0.5
S2	In	10	c1=0.1, c2=0.2, c3=0.7
S3	In	135	c1=0.4, c2=0.1, c3=0.5
S4	Out	unknown	unknown

Apply stream addition to find S4.

# EXAMPLE 6
from pychemengg.massbalances import physicalmassbalance as pmb
mixer1 = pmb.PhysicalProcess("mixer1")

streams = ["S1", "S2", "S3", "S4"]
flowrates = [200, 10, 135, "-F"]
fractions = [[0.2, 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, 0.1, 0.5],["x", "x", "x"]]
S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)
Smix = S1 + S2 + S3
# Output is
    # The following intermediate result is automatically printed for
    # each binary operation: Here it is S1 + S2
    Total flow =  210
    fractions [0.19523809523809524, 0.29523809523809524, 0.5095238095238095]
    # Next it is S1 + S2 + S3
    Total flow =  345
    fractions [0.2753623188405797, 0.21884057971014492, 0.5057971014492754]

print(Smix)
    # This is the result of print(Smix)
    Stream: temp
    Attached to the physical process: TEMPPROCESS
    flowrate: 345
    fractions: [0.2753623188405797, 0.21884057971014492, 0.5057971014492754]
    extrainfo: None
    # Note that for Smix
    # streamname = temp
    # processname = tempprocess
    # User must store the calculated flowrate and fractions into S4

S4.setflow(-(Smix.flowrate))
# Notice negative sign since S4 is exiting the process
S4.setfractions((Smix).fractions)
# print S4 to check
print(S4)
# Output is
    Stream: S4
    Attached to the physical process: MIXER1
    flowrate: -345
    fractions: [0.2753623188405797, 0.21884057971014492, 0.5057971014492754]
    extrainfo: None

# CHECK
# S4-(S1+S3) should give back flowrate and fractions of S2
Ssubtract = S4-(S1+S3)
# Output is
    # The following intermediate result is automatically printed for
    # each binary operation: Here it is (S1 + S3)
    Total flow =  335
    fractions [0.28059701492537314, 0.21940298507462686, 0.5]
    # And this is the result of S4-(S1+S3)
    Total flow =  10
    fractions [0.1, 0.2, 0.7]
    # Indeed these flowrate and fractions are the same as for S2

Example 7: How to `perform degree of freedom analysis`¶

Example 7. Consider streams that enters a mixer.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=0.2, c2=0.3, c3=0.5
S2	In	10	c1=0.1, c2=0.2, c3=0.7
S3	In	135	c1=0.4, c2=0.1, c3=0.5
S4	Out	unknown	unknown

What does the degree of freedom analysis look like?

# EXAMPLE 7
from pychemengg.massbalances import physicalmassbalance as pmb
mixer1 = pmb.PhysicalProcess("mixer1")

streams = ["S1", "S2", "S3", "S4"]
flowrates = [200, 10, 135, "-F"]
fractions = [[0.2, 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, 0.1, 0.5],["x", "x", "x"]]
S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)
# To perform degree of freedom analysis use degreeoffreedom()
mixer1.degreesoffreedom()
# Output is
    ======================================
    Degrees of freedom analysis for MIXER1
    ======================================
    Number of unknown flowrates :--> 1
    Number of unknown 'x' fractions :--> 3
    Total unknowns :--> 4
    --------------------
    Total possible component balances (ΣFx)in = (ΣFx)out :-->  3
    Total possible sum of stream fractions is unity balances (Σx) = 1 :--> 1
    Other extra equations :--> 0
    Total equations :--> 4

    System can be solved

    There are =  4 unknowns and 4 possible equations
    --------------------------------------------
    End of degree of freedom analysis for MIXER1
    --------------------------------------------

Example 8: How to `find unknown flow rate using overall balance`¶

Example 8. Consider streams that enters a mixer.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=0.2, c2=0.3, c3=0.5
S2	In	10	c1=0.1, c2=0.2, c3=0.7
S3	In	135	c1=0.4, c2=0.1, c3=0.5
S4	Out	unknown	unknown

Find the unknown flow rate using overall balance and update the unknown flowrate. Do not use the built in solvesystem() solver.

# EXAMPLE 8
from pychemengg.massbalances import physicalmassbalance as pmb
mixer1 = pmb.PhysicalProcess("mixer1")

streams = ["S1", "S2", "S3", "S4"]
flowrates = [200, 10, 135, "-F"]
fractions = [[0.2, 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, 0.1, 0.5],["x", "x", "x"]]
S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)
# To find unknown flowrate using ΣF = 0, where F = flowrates use find_unknownflowrates()
unknownflow = mixer1.find_unknownflowrate()
print(unknownflow)
# Output is:
    [[True, 'S4', -345.0]]
# To update the stream using the newly found flowrate use update_streamflowrates()
mixer1.update_streamflowrates(unknownflow)
# The following gets printed on screen
    For  " mixer1 " : the stream " S4 " has new flowrate = -345.0
# Confirm S4 has been updated by printing mixer1
print(mixer1)
# Output is:
    ================================
    Process streams for MIXER1 are :
    ================================
    Stream = S1; Flowrate =    200.00; Fractions = ['0.2000', '0.3000', '0.5000']; Extra Info = None
    Stream = S2; Flowrate =     10.00; Fractions = ['0.1000', '0.2000', '0.7000']; Extra Info = None
    Stream = S3; Flowrate =    135.00; Fractions = ['0.4000', '0.1000', '0.5000']; Extra Info = None
    Stream = S4; Flowrate =   -345.00; Fractions = ['  x   ', '  x   ', '  x   ']; Extra Info = None
    --------------------------------
    END

NOTE: This approach only works if there is just one unknown flowrate.

Example 9: How to `find unknown fractions using fraction balance`¶

Example 9. Consider streams that enters a mixer.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=”x”, c2=0.3, c3=0.5
S2	In	10	c1=0.1, c2=0.2, c3=0.7
S3	In	135	c1=0.4, c2=”x”, c3=”x”
S4	Out	-345	c1=0.2753623188405797, c2=0.21884057971014492, c3=”x”

Find the unknown fractions and update the fractions with the new values.

# EXAMPLE 9
from pychemengg.massbalances import physicalmassbalance as pmb
mixer1 = pmb.PhysicalProcess("mixer1")

streams = ["S1", "S2", "S3", "S4"]
flowrates = [200, 10, 135, -345]
fractions = [["x", 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, "x", "x"], [0.2753623188405797, 0.21884057971014492, "x"]]
S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)
# To find unknown fractions using Σx = 1, where x = fractions, use find_unknownfractions()
unknownfractions = mixer1.find_unknownfractions()
print(unknownfractions)
# Output is:
    [[True, 'S1', 0, 0.19999999999999996],
    [False, 'S2', 'There are no missing fractions.'],
    [False, 'S3', "More than one 'x' unknown fractions in the stream. Σx = 1 is insufficient to find them."],
    [True, 'S4', 2, 0.5057971014492754]]
# To update the stream using the newly found fractions use update_streamfractions()
mixer1.update_streamfractions(unknownfractions)
# The following gets printed on screen
    For  " mixer1 " : the stream " S1 " The new component fraction @ position = " 0 " is now =  0.19999999999999996
    For  " mixer1 " : the stream " S2 " There are no missing fractions.
    For  " mixer1 " : the stream " S3 " More than one 'x' unknown fractions in the stream. Σx = 1 is insufficient to find them.
    For  " mixer1 " : the stream " S4 " The new component fraction @ position = " 2 " is now =  0.5057971014492754
# Confirm all streams have been updated by printing mixer1
print(mixer1)
# Output is:
    ================================
    Process streams for MIXER1 are :
    ================================
    Stream = S1; Flowrate =  200.00; Fractions = ['0.2000', '0.3000', '0.5000']; Extra Info = None
    Stream = S2; Flowrate =   10.00; Fractions = ['0.1000', '0.2000', '0.7000']; Extra Info = None
    Stream = S3; Flowrate =  135.00; Fractions = ['0.4000', '  x   ', '  x   ']; Extra Info = None
    Stream = S4; Flowrate = -345.00; Fractions = ['0.2754', '0.2188', '0.5058']; Extra Info = None
    --------------------------------
    END

Example 10: How to `set extra information`¶

Example 10. Sometimes, additional information is given that can help formulate equations besides the following ones:

Overall balance: \(ΣF\) = 0
Component fraction balance: \(Σx\) = 1
Component balance : \((ΣFx)_{in} - (ΣFx)_{out}\) = 0

These equations often represent either:

total mass/mole flowrate relationship between streams, or
mass/mole relationship between components in different streams

Consider the following mixer streams.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=0.2, c2=0.3, c3=0.5
S2	In	10	c1=0.1, c2=0.2, c3=0.7
S3	In	135	c1=0.4, c2=0.1, c3=0.5
S4	Out	unknown	unknown

Express the following relationships:

Flow rate of S1 is 20 times that of S2
Flow rate of component 1 in stream S3 is 1.35 times its flowrate in stream S1

# EXAMPLE 10
from pychemengg.massbalances import physicalmassbalance as pmb
mixer1 = pmb.PhysicalProcess("mixer1")

streams = ["S1", "S2", "S3", "S4"]
flowrates = [200, 10, 135, "-F"]
fractions = [[0.2, 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, 0.1, 0.5],["x", "x", "x"]]
S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)
# Confirm the system is properly set up using print(mixer1)
print(mixer1)
# Output is:
    ================================
    Process streams for MIXER1 are :
    ================================
    Stream = S1; Flowrate = 200.00; Fractions = ['0.2000', '0.3000', '0.5000']; Extra Info = None
    Stream = S2; Flowrate =  10.00; Fractions = ['0.1000', '0.2000', '0.7000']; Extra Info = None
    Stream = S3; Flowrate = 135.00; Fractions = ['0.4000', '0.1000', '0.5000']; Extra Info = None
    Stream = S4; Flowrate =     -F; Fractions = ['  x   ', '  x   ', '  x   ']; Extra Info = None
    --------------------------------
    END

# To set extra info use setextrainfo()
# Flow rate of S2 is 20 times that of S1
S1.setextrainfo(["S1=20*S2"])
# Confirm by printing mixer1
print(mixer1)
# Output is:
    ================================
    Process streams for MIXER1 are :
    ================================
    Stream = S1; Flowrate = 200.00; Fractions = ['0.2000', '0.3000', '0.5000']; Extra Info = ['S1=20*S2']
    Stream = S2; Flowrate =  10.00; Fractions = ['0.1000', '0.2000', '0.7000']; Extra Info = None
    Stream = S3; Flowrate = 135.00; Fractions = ['0.4000', '0.1000', '0.5000']; Extra Info = None
    Stream = S4; Flowrate =     -F; Fractions = ['  x   ', '  x   ', '  x   ']; Extra Info = None
    --------------------------------
    END

# Flow rate of component 1 in stream S3 is 1.35 times its flowrate in stream S1
S3.setextrainfo(["1:S3=1.35*S1"])
# Confirm by printing mixer1
print(mixer1)
# Output is:
    ================================
    Process streams for MIXER1 are :
    ================================
    Stream = S1; Flowrate = 200.00; Fractions = ['0.2000', '0.3000', '0.5000']; Extra Info = ['S1=20*S2']
    Stream = S2; Flowrate =  10.00; Fractions = ['0.1000', '0.2000', '0.7000']; Extra Info = None
    Stream = S3; Flowrate = 135.00; Fractions = ['0.4000', '0.1000', '0.5000']; Extra Info = ['1:S3=1.35*S1']
    Stream = S4; Flowrate =     -F; Fractions = ['  x   ', '  x   ', '  x   ']; Extra Info = None
    --------------------------------
    END

Example 11: How to `use perform_component_massbalance()`¶

Example 11. Consider streams that enter a mixer.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=”x”, c2=0.3, c3=0.5
S2	In	10	c1=0.1, c2=0.2, c3=0.7
S3	In	135	c1=0.4, c2=0.1, c3=”x”
S4	Out	-345	c1=0.2753623188405797, c2=0.21884057971014492, c3=”x”

Perform a component mass balance and find the unknown “x” fractions. Note that there are three unknown fractions, therefore, the three component mass balances \((ΣF_ix_{i,component})\) = 0; where i = stream index, should be sufficient. Do not use built in solvesystem() function.

# EXAMPLE 11
from pychemengg.massbalances import physicalmassbalance as pmb
mixer1 = pmb.PhysicalProcess("mixer1")

# The following methodology is typically used to set up the process.
#
# streams = ["S1", "S2", "S3", "S4"]
# flowrates = [200, 10, 135, -345]
# fractions = [["x", 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, 0.1, "x"], [0.2753623188405797, 0.21884057971014492, "x"]]
# S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)
#
# Implement the above inside a function as shown below.
# define a function that takes x-fractions as input
def massbalances(xfracs):
# There are three unknowns therefore the xfracs will be an array with three elements
# xfracs[0], xfracs[1], xfracs[2]
# Assign them to unknowns below, in any order
    streams = ["S1", "S2", "S3", "S4"]
    flowrates = [200, 10, 135, -345]
    # Assign the xfracs parameter to unknown 'x' locations
    fractions = [[xfracs[0], 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, 0.1, xfracs[1]], [0.2753623188405797, 0.21884057971014492, xfracs[2]]]
    S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)
    balance = mixer1.perform_component_massbalance()
    # perform_component_massbalance()
    # The balance is a numpy array.
    # There are three components, so balance contains three elements.
    # Each element of this array should be zero
    # These each become equations to be solved (meaning each must be made = 0 with the correct choice of xfracs)
    return balance[0], balance[1], balance[2]

# The above function returns the component balance
# Solve the function using a solver.
# The 'leastsq' solver has been found to be most robust
from scipy.optimize import leastsq
# Guess values are needed. Since all unknowns are 'x' mass fractions
# let these each be 0.5
xfrac_guess = [0.5, 0.5, 0.5]
z = leastsq(massbalances, xfrac_guess)
print("The unknowns are:")
print(z[0][0])
print(z[0][1])
print(z[0][2])

# OUTPUT is:
The unknowns are:

0.19999999999999996
0.5
0.5057971014492754

Example 12: How to `find unknown flowrates and fractions`¶

Example 12. Consider streams that enters a mixer.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=”x”, c2=0.3, c3=0.5
S2	In	“F”	c1=0.1, c2=0.2, c3=0.7
S3	In	“F”	c1=0.4, c2=”x”, c3=”x”
S4	Out	-345	c1=0.2753623188405797, c2=0.21884057971014492, c3=”x”

Find the unknown “F” and “x”.

# EXAMPLE 12
from pychemengg.massbalances import physicalmassbalance as pmb
mixer1 = pmb.PhysicalProcess("mixer1")

# The following methodology is used to set up the process.
#
streams = ["S1", "S2", "S3", "S4"]
flowrates = [200, "F", "F", -345]
fractions = [["x", 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, "x", "x"], [0.2753623188405797, 0.21884057971014492, "x"]]
S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)

# Perform degree of freedom analysis
mixer1.degreesoffreedom()

# Output is:
    ======================================
    Degrees of freedom analysis for MIXER1
    ======================================
    Number of unknown flowrates :--> 2
    Number of unknown 'x' fractions :--> 4
    Total unknowns :--> 6
    --------------------
    Total possible component balances (ΣFx)in = (ΣFx)out :-->  3
    Total possible sum of stream fractions is unity balances (Σx) = 1 :--> 3
    Other extra equations :--> 0
    Total equations :--> 6

    System can be solved

    There are =  6 unknowns and 6 possible equations
    --------------------------------------------
    End of degree of freedom analysis for MIXER1
    --------------------------------------------

# Degree of freedom shows the system can be solved
# Implement the above system definition inside a function as shown below.
# Define a function that takes x-fractions and flowrates as input
def massbalances(xf):
# There are six unknowns therefore the xf will be an array with six elements
# xf[0], xf[1], xf[2], xf[3], xf[4], xf[5]
# Assign them to unknowns below, in any order
    streams = ["S1", "S2", "S3", "S4"]
    flowrates = [200, xf[0], xf[1], -345]
    # Assign the xfracs parameter to unknown 'x' locations
    fractions = [[xf[2], 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, xf[3], xf[4]], [0.2753623188405797, 0.21884057971014492, xf[5]]]
    S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)

    # There are six unknowns, therefore, six equations are needed
    # Three will be the three component balances
    componentbalance = mixer1.perform_component_massbalance()
    # The balance is a numpy array.
    # There are three components, so balance contains three elements: componentbalance[0], componentbalance[1], componentbalance[2]
    # Each element of this array should be zero
    # These each become equations to be solved (meaning each must be made = 0 with the correct choice of xf)
    # Thus equations to solve become
    # componentbalance[0] = 0   ...... (1)
    # componentbalance[1] = 0   ...... (2)
    # componentbalance[2] = 0   ...... (3)

    # The other three equations are going to be (Σx) = 1 for each stream
    fractionsums = [sum(x) for x in fractions]
    # This will make a list with each element being the sum of fractions for each stream.
    # Since there are four streams, there are four elements in fractionsums
    # fractionsums[0], fractionsums[1], fractionsums[2], fractionsums[3]
    # Out of these four, the ones that have unknown 'x' should be selected
    # Thus fractionsums[1] is not selected
    # Equations to solve become
    # fractionsums[0] - 1 = 0   ...... (4)
    # fractionsums[2] - 1 = 0   ...... (5)
    # fractionsums[3] - 1 = 0   ...... (6)
    # Return equations 1 through 6
    return componentbalance[0], componentbalance[1], componentbalance[2],fractionsums[0] - 1, fractionsums[2] - 1, fractionsums[3] - 1


# The above function returns the equations
# Solve the function using a solver.
# The 'leastsq' solver has been found to be most robust
from scipy.optimize import leastsq
# Guess values are needed. Since first two xf are assigned to flowrate and remaining to 'x'
# Let guess be
xf_guess = [200, 345, 0.5, 0.5, 0.5, 0.5]
z = leastsq(massbalances, xf_guess)
print("The unknowns are:")
print(z[0][0])
print(z[0][1])
print(z[0][2])
print(z[0][3])
print(z[0][4])
print(z[0][5])

# OUTPUT is:
The unknowns are:
9.999999999999952 # flowrate of S2
135.00000000000003 # flowrate of S3
0.19999999999999996 # fraction of S1
0.09999999999999996 # fraction of S3
0.5000000000000003 # fraction of S3
0.5057971014492755 # fraction of S4
# User should look at the function and track what each variable means

Example 13: How to `use built in solvesystem()`¶

Example 13. Consider streams that enter a mixer.

Stream name	In/Out	Flowrate (kg/s)	Component mass fraction
S1	In	200	c1=”x”, c2=0.3, c3=0.5
S2	In	“F”	c1=0.1, c2=0.2, c3=0.7
S3	In	“F”	c1=0.4, c2=”x”, c3=”x”
S4	Out	-345	c1=0.2753623188405797, c2=0.21884057971014492, c3=”x”

Find the unknown “F” and “x” using built in solver solvesystem().

# EXAMPLE 13
from pychemengg.massbalances import physicalmassbalance as pmb
mixer1 = pmb.PhysicalProcess("mixer1")
# Set up the process.
streams = ["S1", "S2", "S3", "S4"]
flowrates = [200, "F", "F", -345]
fractions = [["x", 0.3, 0.5], [0.1, 0.2, 0.7], [0.4, "x", "x"], [0.2753623188405797, 0.21884057971014492, "x"]]
S1, S2, S3, S4 = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)

# Solve using solvesystem() function
solution = mixer1.solvesystem()
# OUTPUT is:
    ======================================
    Degrees of freedom analysis for MIXER1
    ======================================
    Number of unknown flowrates :--> 2
    Number of unknown 'x' fractions :--> 4
    Total unknowns :--> 6
    --------------------
    Total possible component balances (ΣFx)in = (ΣFx)out :-->  3
    Total possible sum of stream fractions is unity balances (Σx) = 1 :--> 3
    Other extra equations :--> 0
    Total equations :--> 6

    System can be solved

    There are =  6 unknowns and 6 possible equations
    --------------------------------------------
    End of degree of freedom analysis for MIXER1
    --------------------------------------------


    Unknowns successfully computed:
    -------------------------------
    Streams with new data have been created.
    You can view the solved system by printing the returned object.

print(solution) # Here solution is the returned object
# OUTPUT is:
    ============================================
    Process streams for SOLUTION TO MIXER1 are :
    ============================================
    Stream = S1; Flowrate =    200.00; Fractions = ['0.2000', '0.3000', '0.5000']; Extra Info = None
    Stream = S2; Flowrate =     10.00; Fractions = ['0.1000', '0.2000', '0.7000']; Extra Info = None
    Stream = S3; Flowrate =    135.00; Fractions = ['0.4000', '0.1000', '0.5000']; Extra Info = None
    Stream = S4; Flowrate =   -345.00; Fractions = ['0.2754', '0.2188', '0.5058']; Extra Info = None
    --------------------------------------------
    END

Example 14: How to `solve continuous process`¶

Example 14. 10 kg/s of a 5% (by wt) ethanol (E) solutions is produced by mixing two streams from two tanks that contain 1% and 41% ethanol, respectively (rest is water (W)) all on weight basis. How much is needed from each tank?

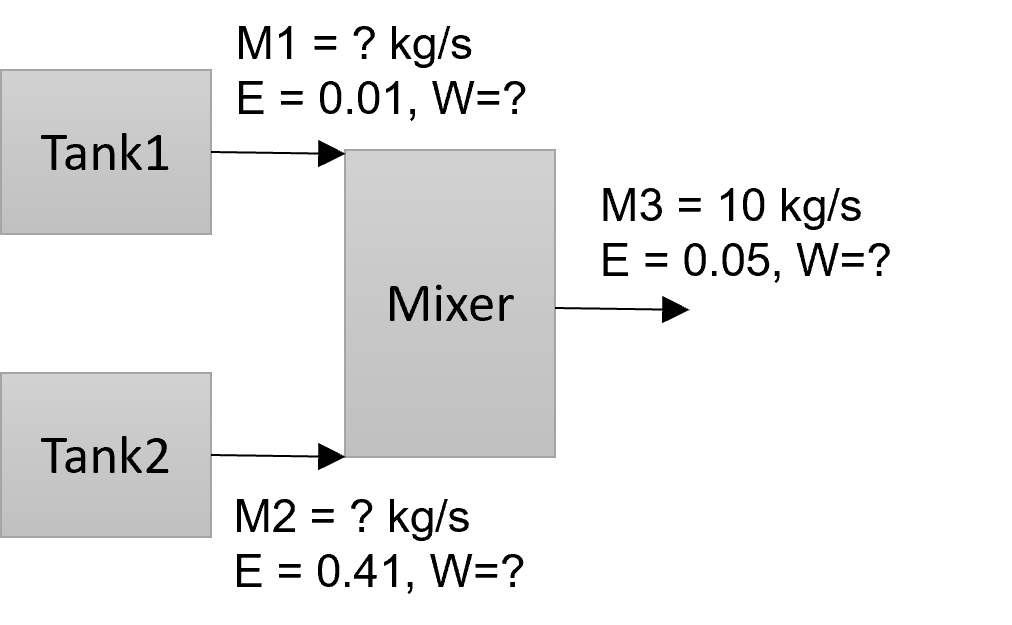
../../_images/continuous_ethanol_mixer.png

Find the unknown flowrates and weight fractions.

# EXAMPLE 14
from pychemengg.massbalances import physicalmassbalance as pmb
ethanolmixer = pmb.PhysicalProcess("ethanolmixer")
# Set up the process.
streams = ["M1", "M2", "M3"]
flowrates = ["F", "F", -10]
fractions = [[0.01,"x"], [0.41,"x"], [0.05, "x"]]
M1, M2, M3 = ethanolmixer.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)

# Solve using solvesystem() function
solution = ethanolmixer.solvesystem()
# OUTPUT is:
    ============================================
    Degrees of freedom analysis for ETHANOLMIXER
    ============================================
    Number of unknown flowrates :--> 2
    Number of unknown 'x' fractions :--> 3
    Total unknowns :--> 5
    --------------------
    Total possible component balances (ΣFx)in = (ΣFx)out :-->  2
    Total possible sum of stream fractions is unity balances (Σx) = 1 :--> 3
    Other extra equations :--> 0
    Total equations :--> 5

    System can be solved

    There are =  5 unknowns and 5 possible equations
    --------------------------------------------------
    End of degree of freedom analysis for ETHANOLMIXER
    --------------------------------------------------


    Unknowns successfully computed:
    -------------------------------
    Streams with new data have been created.
    You can view the solved system by printing the returned object.

print(solution) # Here solution is the returned object

# OUTPUT is:
    ==================================================
    Process streams for SOLUTION TO ETHANOLMIXER are :
    ==================================================
    Stream = M1; Flowrate =     9.00; Fractions = ['0.0100', '0.9900']; Extra Info = None
    Stream = M2; Flowrate =     1.00; Fractions = ['0.4100', '0.5900']; Extra Info = None
    Stream = M3; Flowrate =   -10.00; Fractions = ['0.0500', '0.9500']; Extra Info = None
    --------------------------------------------------
    END

Example 15: How to `solve batch process`¶

Example 15. From clean water and an aqueous solution with 5% S(NaCl), we want to produce 1 kg of 2% NaCl (all weight %). How much of each stream is required?

Find the unknown flowrates and weight fractions.

# EXAMPLE 15
from pychemengg.massbalances import physicalmassbalance as pmb
saltmixer = pmb.PhysicalProcess("saltmixer")
# Set up the process.
streams = ["water", "salt", "product"]
flowrates = ["F", "F", -1]
fractions = [[0.0,1], [0.05,"x"], [0.02, "x"]]
water, salt, product = saltmixer.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)

# Solve using solvesystem() function
solution = saltmixer.solvesystem()
# OUTPUT is:
    =========================================
    Degrees of freedom analysis for SALTMIXER
    =========================================
    Number of unknown flowrates :--> 2
    Number of unknown 'x' fractions :--> 2
    Total unknowns :--> 4
    --------------------
    Total possible component balances (ΣFx)in = (ΣFx)out :-->  2
    Total possible sum of stream fractions is unity balances (Σx) = 1 :--> 2
    Other extra equations :--> 0
    Total equations :--> 4

    System can be solved

    There are =  4 unknowns and 4 possible equations
    -----------------------------------------------
    End of degree of freedom analysis for SALTMIXER
    -----------------------------------------------


    Unknowns successfully computed:
    -------------------------------
    Streams with new data have been created.
    You can view the solved system by printing the returned object.

print(solution)  # Here solution is the returned object
# OUTPUT is:
    ===============================================
    Process streams for SOLUTION TO SALTMIXER are :
    ===============================================
    Stream = water  ; Flowrate =    0.60; Fractions = ['0.0000', '1.0000']; Extra Info = None
    Stream = salt   ; Flowrate =    0.40; Fractions = ['0.0500', '0.9500']; Extra Info = None
    Stream = product; Flowrate =   -1.00; Fractions = ['0.0200', '0.9800']; Extra Info = None
    -----------------------------------------------
    END

Example 16: How to `solve multiple processes with extra info and recycle`¶

Example 16. 5000 kg/h of an aqueous solution with 20% (all weight %) potassium salt (abbreviated as K) is mixed with a recycle stream. This is then sent to an evaporator to remove water such that the outlet from evaporator contains 35% K. This stream is then sent to crystallization/filtration units. The filtrate with 30% K is recycled. The product comprises the crystals (filter cake), which is mostly solid crystals (K) and filtrate stream. The filtrate stream comprises 1/26th of the total product.

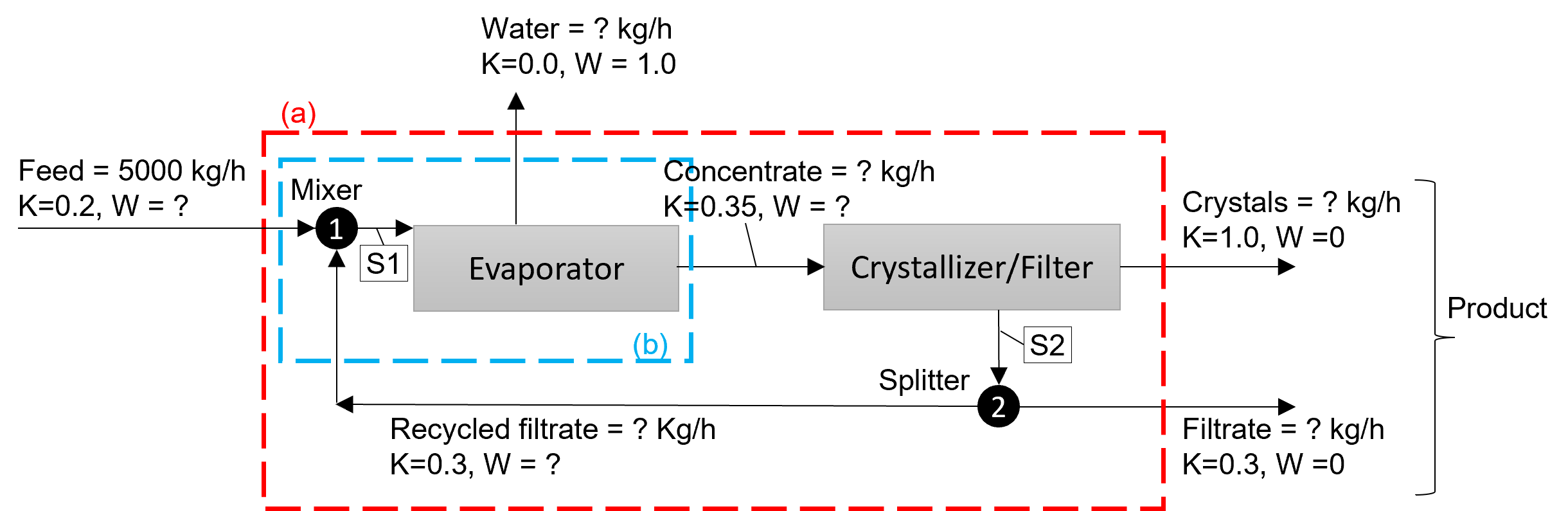
../../_images/multiple_processes_with_recycle.png

Find the unknown flowrates and weight fractions.

SOLUTION:

To solve this problem,

first define the different processes and assign the streams
perform degree of freedom analysis to determine what part can be solved
solve that portion
again perform degree of freedom analysis to see what parts can be solved
repeat the process until unknowns are computed.
NOTE: extrainfo is given as: Filtrate = 1/26(Filtrate + Crystals)
This can be simplified to : Crystals = 25*Filtrate
The extrainfo can be attached to any stream really, but it makes sense if it is attached to Filtrate or Crystals
We will attach it to Crystals

# EXAMPLE 16
from pychemengg.massbalances import physicalmassbalance as pmb
# define all processes
mixer1 = pmb.PhysicalProcess("mixer1")
evaporator = pmb.PhysicalProcess("evaporator")
crystallizer = pmb.PhysicalProcess("crystallizer")
splitter2 = pmb.PhysicalProcess("splitter2")
# Also define an overall process (red line - (a) in figure)
overall = pmb.PhysicalProcess("overall")
# And define for boundary (b) over evaporator  + mixer1
evap_mixer1 = pmb.PhysicalProcess("evap_mixer1")

# Now assign streams to each process
# for mixer1
streams = ["feed", "recyclefiltrate_in", "s1_out"]
flowrates = [5000, "F", "-F"]
fractions = [[0.2, "x"], [0.3, "x"], ["x", "x"]]
mixer1.feed, mixer1.recyclefiltrate_in, mixer1.s1_out = mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)
# NOTE the use of dot operator so that it is convenient to track which stream
# belongs to which process.

#for evaporator
streams = ["s1_in", "water", "concentrate_out"]
flowrates = ["F", "-F", "-F"]
fractions = [["x", "x"], [0, 1], [0.35, "x"]]
evaporator.s1_in, evaporator.water, evaporator.concentrate_out = evaporator.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)

#for crystallizer
streams = ["concentrate_in", "s2_out", "crystals"]
flowrates = ["F", "-F", "-F"]
fractions = [[0.35, "x"], [0.3, "x"], [1, 0]]
crystallizer.concentrate_in, crystallizer.s2_out, crystallizer.crystals = crystallizer.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)

#for splitter 2
streams = ["s2_in", "recyclefiltrate_out", "filtrate"]
flowrates = ["F", "-F", "-F"]
fractions = [[0.3, "x"], [0.3, "x"], [0.3, "x"]]
splitter2.s2_in, splitter2.recyclefiltrate_out, splitter2.filtrate = splitter2.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)

# overall ... boundary (a)
streams = ["feed", "water", "crystals", "filtrate"]
flowrates = [5000, "-F", "-F", "-F"]
fractions = [[0.2, "x"], [0, 1], [1, 0], [0.3, "x"]]
extrainfo = [[], [], [], ["crystals=25*filtrate"]]
overall.feed, overall.water, overall.crystals, overall.filtrate = overall.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions, extrainfos=extrainfo)

# evap_mixer1 ... boundary (b)
streams = ["feed", "recyclefiltrate_in", "water", "concentrate_out"]
flowrates = [5000, "F", "-F", "-F"]
fractions = [[0.2, "x"], [0.3, "x"], [0, 1], [0.35, "x"]]
evap_mixer1.feed, evap_mixer1.recyclefiltrate_in, evap_mixer1.water, evap_mixer1.concentrate_out = evap_mixer1.attachstreams(streamnames=streams, flowrates=flowrates, fractions=fractions)


# perform degrees of freedom on all systems
overall.degreesoffreedom()
splitter2.degreesoffreedom()
crystallizer.degreesoffreedom()
evaporator.degreesoffreedom()
mixer1.degreesoffreedom()
evap_mixer1.degreesoffreedom()

# From degree of freedom analysis it is clear only "overall"
# can be solved. Therefore, solve "overall" first.
overall_solution = overall.solvesystem()
# Print the original "overall" system
print(overall)
# Print the solution to overall
print(overall_solution)

# # To find the other unknowns one must use streams computed from
# # "overall_solution" to update information of other streams.
# # Thus, update "feed", "water", "filtrate" and "crystals" streams
# # that interconnect processes.
# # The setequalto() function can be used for this purpose
mixer1.feed.setequalto(overall_solution.feed, flowdirection="+")
evaporator.water.setequalto(overall_solution.water, flowdirection="-")
crystallizer.crystals.setequalto(overall_solution.crystals, flowdirection="-")
splitter2.filtrate.setequalto(overall_solution.filtrate, flowdirection="-")
evap_mixer1.water.setequalto(overall_solution.water, flowdirection="-")

# Again perform degree of freedom analysis
splitter2.degreesoffreedom()
crystallizer.degreesoffreedom()
evaporator.degreesoffreedom()
mixer1.degreesoffreedom()
evap_mixer1.degreesoffreedom()

# The degree of freedom analysis shows that splitter2, crystallizer, and evap_mixer1 can be solved
# First print them to check
print(crystallizer)
print(splitter2)
print(evap_mixer1)

# Solve these systems
splitter2_soln = splitter2.solvesystem()
crystallizer_soln = crystallizer.solvesystem()
evap_mixer1_soln = evap_mixer1.solvesystem()

# print the solutions
print(splitter2_soln)
print(crystallizer_soln)
print(evap_mixer1_soln)

# One stream is connecting crystallizer and evaporator
# and this is concentrate_out <-----> concentrate_in
# This stream has the same flowrate when independently
# the evap_mixer1 and crystallizer are solved.
# Similarly, crystallizer and splitter2 are connected via
# s2_out <-----> s2_in.
# This stream gave different results for the crystallizer and splitter2
# This means the splitter2 system solution is not correct.

# Use the data from crystallizer and evap_mixer1 solutions to complete
# other stream data.

mixer1.recyclefiltrate_in.setequalto(evap_mixer1_soln.recyclefiltrate_in, flowdirection="+")
splitter2.recyclefiltrate_out.setequalto(evap_mixer1_soln.recyclefiltrate_in, flowdirection="-")
splitter2.s2_in.setequalto(crystallizer_soln.s2_out, flowdirection = "+")



# Again perform degree of freedom analysis
splitter2.degreesoffreedom()
mixer1.degreesoffreedom()

# Degree of analysis shows splitter2 is already fully solved
# and mixer1 is solvable

# Print them first
print(splitter2)
print(mixer1)

# Solve mixer1
mixer1_soln = mixer1.solvesystem()
# Print mixer1 solution
print(mixer1_soln)
# This completes the solution

Example 17: Example `mixer with extra info`¶

Example 17. Pure water is mixed with 1000 kg/h of pure NaOH to produce product. The water flow rate is 0.9 times the flow rate of the product.

Find the unknown flowrates and weight fractions.

SOLUTION:

# EXAMPLE 17
from pychemengg.massbalances import physicalmassbalance as pmb
# define mixer
Mixer_NaOH = pmb.PhysicalProcess("Mixer_NaOH")
# Attach streams
# In this example each stream is attached one at a time
Mixer_NaOH.Water = Mixer_NaOH.attachstreams(streamnames=["Water"])
Mixer_NaOH.Water.setflow("F")
Mixer_NaOH.Water.setfractions([1,0])
Mixer_NaOH.Water.setextrainfo(["Water=0.9*Product"])
# The extra information can be attached to any stream.
# Here it is attached to 'Water' stream.
# User can attach it to other streams to test the result.
Mixer_NaOH.NaOH = Mixer_NaOH.attachstreams(streamnames=["NaOH"])
Mixer_NaOH.NaOH.setflow(1000)
Mixer_NaOH.NaOH.setfractions([0,1])
Mixer_NaOH.Product = Mixer_NaOH.attachstreams(streamnames=["Product"])
Mixer_NaOH.Product.setflow("-F")
Mixer_NaOH.Product.setfractions(["x", "x"])

print(Mixer_NaOH)
#Output is:
====================================
Process streams for MIXER_NAOH are :
====================================
Stream = Water  ; Flowrate =       F; Fractions = ['1.0000', '0.0000']; Extra Info = ['Water=0.9*Product']
Stream = NaOH   ; Flowrate = 1000.00; Fractions = ['0.0000', '1.0000']; Extra Info = None
Stream = Product; Flowrate =      -F; Fractions = ['  x   ', '  x   ']; Extra Info = None
------------------------------------
END

sol = Mixer_NaOH.solvesystem()
# Output is:
    ==========================================
    Degrees of freedom analysis for MIXER_NAOH
    ==========================================
    Number of unknown flowrates :--> 2
    Number of unknown 'x' fractions :--> 2
    Total unknowns :--> 4
    --------------------
    Total possible component balances (ΣFx)in = (ΣFx)out :-->  2
    Total possible sum of stream fractions is unity balances (Σx) = 1 :--> 1
    Other extra equations :--> 1
    Total equations :--> 4

    System can be solved

    There are =  4 unknowns and 4 possible equations
    ------------------------------------------------
    End of degree of freedom analysis for MIXER_NAOH
    ------------------------------------------------


    Unknowns successfully computed:
    -------------------------------
    Streams with new data have been created.
    You can view the solved system by printing the returned object.

print(sol)
# Output is:
    ================================================
    Process streams for SOLUTION TO MIXER_NAOH are :
    ================================================
    Stream = Water  ; Flowrate =     9000.00; Fractions = ['1.0000', '0.0000']; Extra Info = ['Water=0.9*Product']
    Stream = NaOH   ; Flowrate =     1000.00; Fractions = ['0.0000', '1.0000']; Extra Info = None
    Stream = Product; Flowrate =   -10000.00; Fractions = ['0.9000', '0.1000']; Extra Info = None
    ------------------------------------------------
    END

Example 18: Example `distillation column - multiple feeds`¶

Example 18. In a distillation column, methanol is separated from water. The column has two feeds and three outlet streams as shown in the schematic.

Find the unknown flowrates and mole fractions.

SOLUTION:

# EXAMPLE 18
from pychemengg.massbalances import physicalmassbalance as pmb
distcolumn = pmb.PhysicalProcess("Distillation Column")
distcolumn.feed1 = distcolumn.attachstreams(streamnames=["feed1"])
distcolumn.feed2 = distcolumn.attachstreams(streamnames=["feed2"])
distcolumn.methanolproduct = distcolumn.attachstreams(streamnames=["methanolproduct"])
distcolumn.fuselproduct = distcolumn.attachstreams(streamnames=["fuselproduct"])
distcolumn.waterproduct = distcolumn.attachstreams(streamnames=["waterproduct"])
distcolumn.feed1.setflow(800)
distcolumn.feed1.setfractions([0.7, 0.2993, 0.0007])
distcolumn.feed2.setflow("F")
distcolumn.feed2.setfractions([0.2, 0.8, 0])
distcolumn.methanolproduct.setflow(-700)
distcolumn.methanolproduct.setfractions([0.995, 0.005, 0])
distcolumn.fuselproduct.setflow("-F")
distcolumn.fuselproduct.setfractions([0.002, "x", 0.045,])
distcolumn.waterproduct.setflow("-F")
distcolumn.waterproduct.setfractions([0.002, 0.998, 0])
print(distcolumn)

#Output is:
    =============================================
    Process streams for DISTILLATION COLUMN are :
    =============================================
    Stream = feed1          ; Flowrate =  800.00; Fractions = ['0.7000', '0.2993', '0.0007']; Extra Info = None
    Stream = feed2          ; Flowrate =       F; Fractions = ['0.2000', '0.8000', '0.0000']; Extra Info = None
    Stream = methanolproduct; Flowrate = -700.00; Fractions = ['0.9950', '0.0050', '0.0000']; Extra Info = None
    Stream = fuselproduct   ; Flowrate =      -F; Fractions = ['0.0020', '  x   ', '0.0450']; Extra Info = None
    Stream = waterproduct   ; Flowrate =      -F; Fractions = ['0.0020', '0.9980', '0.0000']; Extra Info = None
    ---------------------------------------------
    END

distcolumn.sol = distcolumn.solvesystem()

# Output is:
    ===================================================
    Degrees of freedom analysis for DISTILLATION COLUMN
    ===================================================
    Number of unknown flowrates :--> 3
    Number of unknown 'x' fractions :--> 1
    Total unknowns :--> 4
    --------------------
    Total possible component balances (ΣFx)in = (ΣFx)out :-->  3
    Total possible sum of stream fractions is unity balances (Σx) = 1 :--> 1
    Other extra equations :--> 0
    Total equations :--> 4

    System can be solved

    There are =  4 unknowns and 4 possible equations
    ---------------------------------------------------------
    End of degree of freedom analysis for DISTILLATION COLUMN
    ---------------------------------------------------------


    Unknowns successfully computed:
    -------------------------------
    Streams with new data have been created.
    You can view the solved system by printing the returned object.

print(distcolumn.sol)
# Output is:
    =========================================================
    Process streams for SOLUTION TO DISTILLATION COLUMN are :
    =========================================================
    Stream = feed1          ; Flowrate =     800.00; Fractions = ['0.7000', '0.2993', '0.0007']; Extra Info = None
    Stream = feed2          ; Flowrate =     690.40; Fractions = ['0.2000', '0.8000', '0.0000']; Extra Info = None
    Stream = methanolproduct; Flowrate =    -700.00; Fractions = ['0.9950', '0.0050', '0.0000']; Extra Info = None
    Stream = fuselproduct   ; Flowrate =     -12.44; Fractions = ['0.0020', '0.9530', '0.0450']; Extra Info = None
    Stream = waterproduct   ; Flowrate =    -777.96; Fractions = ['0.0020', '0.9980', '0.0000']; Extra Info = None
    ---------------------------------------------------------
    END

Example 19: Example `distillation column - extra info`¶

Example 19. A distillation column has two feeds and three outlet streams as shown in the schematic. Two additional pieces of information are provided as indicated under “Other relationships”.

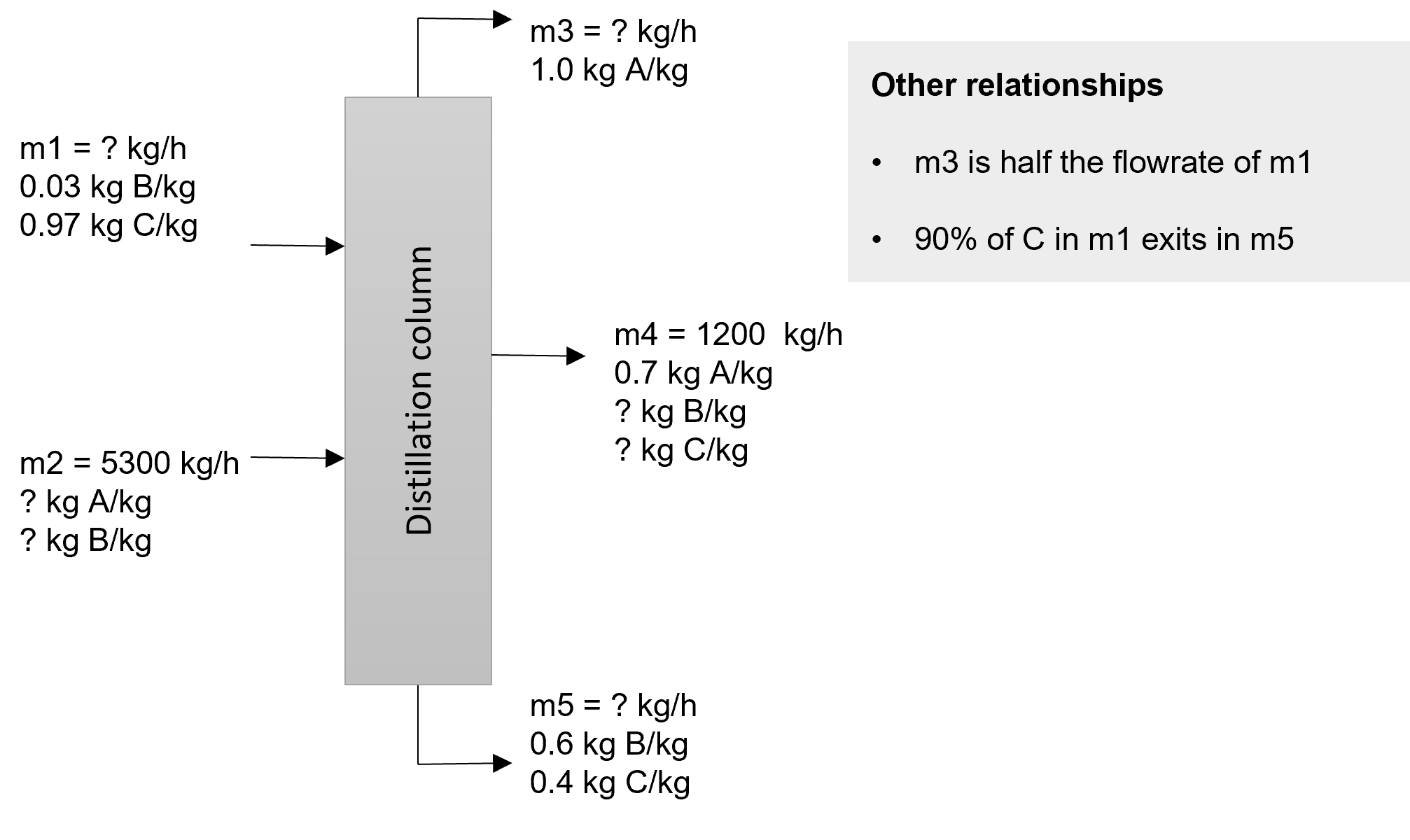
../../_images/distillation_column_extra_info.png

Find the unknown flowrates and mass fractions.

Youtube solution example 19

SOLUTION:

# EXAMPLE 19

from pychemengg.massbalances import physicalmassbalance as pmb
distillationcolumn=pmb.PhysicalProcess("Distillation Column")
m1 = distillationcolumn.attachstreams(streamnames=["m1"] )
m1.setflow("F")
m1.setfractions( [0, 0.03, 0.97] )
m2 = distillationcolumn.attachstreams(streamnames=["m2"])
m2.setflow(5300)
m2.setfractions( ["x", "x", 0] )
m3 = distillationcolumn.attachstreams( streamnames=["m3"] )
m3.setflow("-F")
m3.setfractions([1, 0, 0])
m3.setextrainfo(["m3=0.5*m1"])
m4 = distillationcolumn.attachstreams( streamnames=["m4"] )
m4.setflow(-1200)
m4.setfractions([0.7, "x", "x"])
m5 = distillationcolumn.attachstreams( streamnames=["m5"] )
m5.setflow("-F")
m5.setfractions([0, 0.6, 0.4])
m5.setextrainfo(["3:m5=0.90*m1"])
print(distillationcolumn)
# Output is:
    =============================================
    Process streams for DISTILLATION COLUMN are :
    =============================================
    Stream = m1; Flowrate =        F; Fractions = ['0.0000', '0.0300', '0.9700']; Extra Info = None
    Stream = m2; Flowrate =  5300.00; Fractions = ['  x   ', '  x   ', '0.0000']; Extra Info = None
    Stream = m3; Flowrate =       -F; Fractions = ['1.0000', '0.0000', '0.0000']; Extra Info = ['m3=0.5*m1']
    Stream = m4; Flowrate = -1200.00; Fractions = ['0.7000', '  x   ', '  x   ']; Extra Info = None
    Stream = m5; Flowrate =       -F; Fractions = ['0.0000', '0.6000', '0.4000']; Extra Info = ['3:m5=0.90*m1']
    ---------------------------------------------
    END

sol = distillationcolumn.solvesystem()
# Output is:
    ===================================================
    Degrees of freedom analysis for DISTILLATION COLUMN
    ===================================================
    Number of unknown flowrates :--> 3
    Number of unknown 'x' fractions :--> 4
    Total unknowns :--> 7
    --------------------
    Total possible component balances (ΣFx)in = (ΣFx)out :-->  3
    Total possible sum of stream fractions is unity balances (Σx) = 1 :--> 2
    Other extra equations :--> 2
    Total equations :--> 7

    System can be solved

    There are =  7 unknowns and 7 possible equations
    ---------------------------------------------------------
    End of degree of freedom analysis for DISTILLATION COLUMN
    ---------------------------------------------------------


    Unknowns successfully computed:
    -------------------------------
    Streams with new data have been created.
    You can view the solved system by printing the returned object.

print(sol)
# Output is:
    =========================================================
    Process streams for SOLUTION TO DISTILLATION COLUMN are :
    =========================================================
    Stream = m1; Flowrate =     2436.85; Fractions = ['0.0000', '0.0300', '0.9700']; Extra Info = None
    Stream = m2; Flowrate =     5300.00; Fractions = ['0.3884', '0.6116', '0.0000']; Extra Info = None
    Stream = m3; Flowrate =    -1218.42; Fractions = ['1.0000', '0.0000', '0.0000']; Extra Info = ['m3=0.5*m1']
    Stream = m4; Flowrate =    -1200.00; Fractions = ['0.7000', '0.1030', '0.1970']; Extra Info = None
    Stream = m5; Flowrate =    -5318.42; Fractions = ['0.0000', '0.6000', '0.4000']; Extra Info = ['3:m5=0.90*m1']
    ---------------------------------------------------------
    END

Example 20: Example `extraction-distillation with extra info`¶

Example 20. In a two stage process, acetic acid (A) is extracted from water (W) into hexanol (H) in aliquid-liquid extraction vessel and the extract is subsequently separated by distillation. Assume that water is completely insoluble in hexanol. A mixture of 18% wt% acetic acid and the balance water is fed to aliquid-liquid extraction vessel. Pure hexanol is fed to the extractor to extract the acetic acid. The water-rich stream leaving the vessel is 99.5 wt% water and the balance acetic acid. The hexanol-rich extract from the extractor is fed to a distillation column. The composition of the distillate is 96 wt% acetic acid and the balance hexanol. The bottoms stream contains 97.2 wt% hexanol and recovers 95% of the hexanol fed to the liquid-liquid extraction vessel. Calculate the percentage of acetic acid in the process feed that is recovered in the distillate stream. Also, find the unknown flowrates and mass fractions.

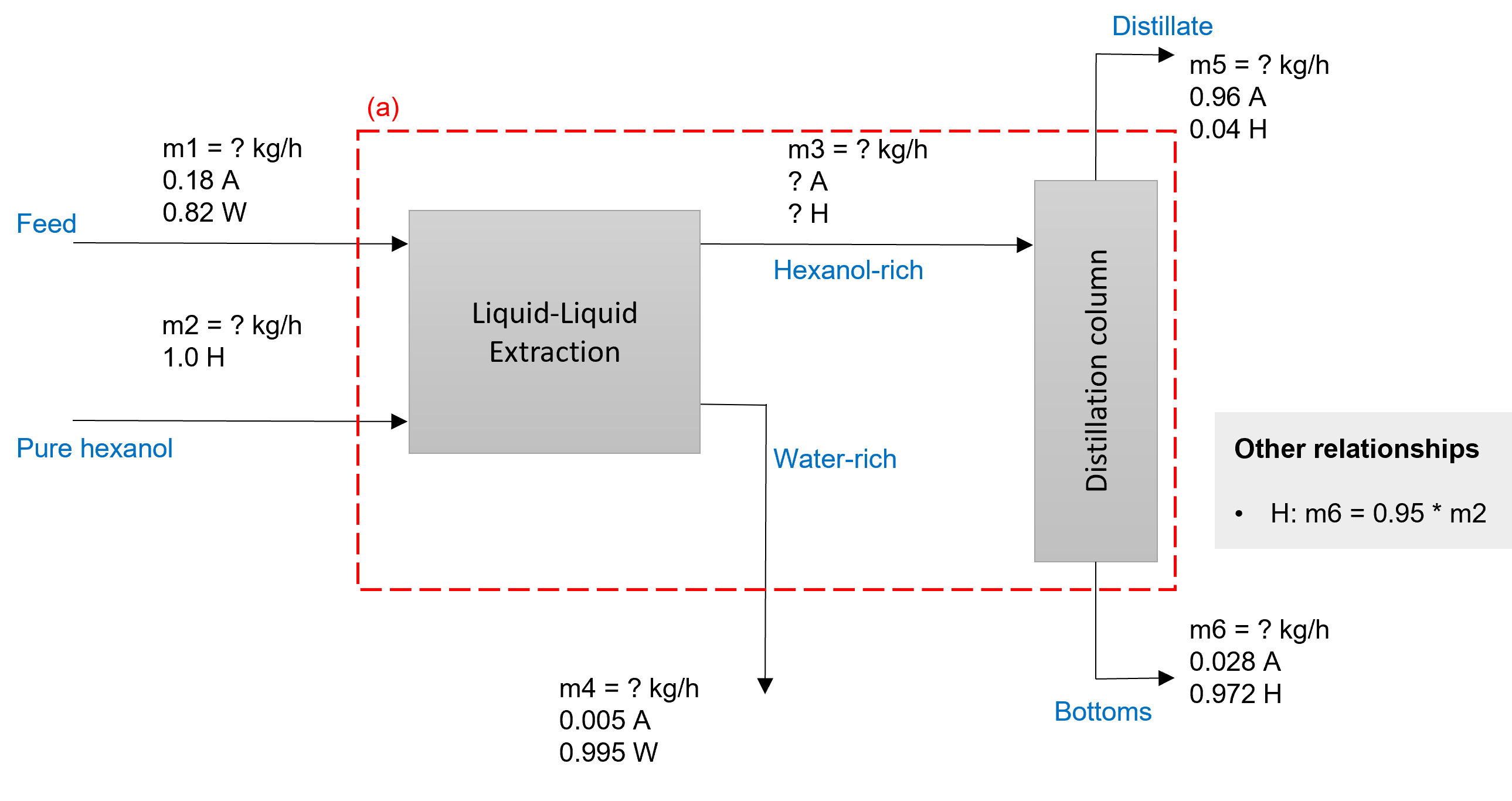
../../_images/extraction_distillation_with_extra_info.png

Youtube solution example 20

SOLUTION:

# EXAMPLE 20

from pychemengg.massbalances import physicalmassbalance as pmb

# Define processes
extraction = pmb.PhysicalProcess("Liquid-Liquid Extraction")
distillation = pmb.PhysicalProcess("Distillation")
overall = pmb.PhysicalProcess("Overall") # dashed boundary (a) in figure

# Assign streams to processes
extraction.m1_in = extraction.attachstreams(streamnames=["m1_in"])
extraction.m1_in.setflow("+F")
# Component mapping:
# position 1: Acetic Acid, position 2: Water, position 3: Hexanol
extraction.m1_in.setfractions([0.18, 0.82, 0])

extraction.m2_in = extraction.attachstreams(streamnames=["m2_in"])
extraction.m2_in.setflow("+F")
extraction.m2_in.setfractions([0, 0, 1.00])

extraction.m3_out = extraction.attachstreams(streamnames=["m3_out"])
extraction.m3_out.setflow("-F")
extraction.m3_out.setfractions(["x", 0, "x"])

extraction.m4_out = extraction.attachstreams(streamnames=["m4_out"])
extraction.m4_out.setflow("-F")
extraction.m4_out.setfractions([0.005, 0.995, 0])

distillation.m3_in = distillation.attachstreams(streamnames=["m3_in"])
distillation.m3_in.setequalto(extraction.m3_out, flowdirection="+")

distillation.m5_out = distillation.attachstreams(streamnames=["m5_out"])
distillation.m5_out.setflow("-F")
distillation.m5_out.setfractions([0.96, 0, 0.04])

distillation.m6_out = distillation.attachstreams(streamnames=["m6_out"])
distillation.m6_out.setflow("-F")
distillation.m6_out.setfractions([0.028, 0, 0.972])
distillation.m6_out.setextrainfo(["3:m6_out=0.95*m2_in"])

overall.m1_in = overall.attachstreams(streamnames=["m1_in"])
overall.m2_in = overall.attachstreams(streamnames=["m2_in"])
overall.m4_out = overall.attachstreams(streamnames=["m4_out"])
overall.m5_out = overall.attachstreams(streamnames=["m5_out"])
overall.m6_out = overall.attachstreams(streamnames=["m6_out"])
# Use setequalto() method to assign stream data
overall.m1_in.setequalto(extraction.m1_in, flowdirection="+")
overall.m2_in.setequalto(extraction.m2_in, flowdirection="+")
overall.m4_out.setequalto(extraction.m4_out, flowdirection="-")
overall.m5_out.setequalto(distillation.m5_out, flowdirection="-")
overall.m6_out.setequalto(distillation.m6_out, flowdirection="-")

# Print streams to verify they are defined correctly
print(extraction)
print(distillation)
print(overall)
# Output not shown here to conserve space

# Perform degree of freedom analysis
extraction.degreesoffreedom()
distillation.degreesoffreedom()
overall.degreesoffreedom()

# From degree of freedom analysis it is clear that none
# of the processes have degree of freedom = 0.
# Therefore, as such the system cannot be solved.
# However, for the 'overall; process the degree of freedom = 1.
# If one of the flow rate is assumed, this will allow the
# process to be solved.
# Thus let m2 = 100
overall.m2_in.setflow(100)

# Check degrees of freedom again
overall.degreesoffreedom()
# The analysis now shows that "overall" system can now be solved.
overall_solution = overall.solvesystem()
print(overall_solution)
# Output is:
    =============================================
    Process streams for SOLUTION TO OVERALL are :
    =============================================
    Stream = m1_in ; Flowrate =     697.85; Fractions = ['0.1800', '0.8200', '0.0000']; Extra Info = None
    Stream = m2_in ; Flowrate =     100.00; Fractions = ['0.0000', '0.0000', '1.0000']; Extra Info = None
    Stream = m4_out; Flowrate =    -575.11; Fractions = ['0.0050', '0.9950', '0.0000']; Extra Info = None
    Stream = m5_out; Flowrate =    -125.00; Fractions = ['0.9600', '0.0000', '0.0400']; Extra Info = None
    Stream = m6_out; Flowrate =     -97.74; Fractions = ['0.0280', '0.0000', '0.9720']; Extra Info = ['3:m6_out=0.95*m2_in']
    ---------------------------------------------
    END

# All streams except m3 are now known.
# Use solution of "overall" system to update streams attached to other processes/systems.
# Update the extraction streams
extraction.m1_in.setequalto(overall_solution.m1_in, flowdirection="+")
extraction.m2_in.setequalto(overall_solution.m2_in, flowdirection="+")
extraction.m4_out.setequalto(overall_solution.m4_out, flowdirection="-")
# Check system streams are correctly defined
print(extraction)
# Output is:
    ==================================================
    Process streams for LIQUID-LIQUID EXTRACTION are :
    ==================================================
    Stream = m1_in ; Flowrate =     697.85; Fractions = ['0.1800', '0.8200', '0.0000']; Extra Info = None
    Stream = m2_in ; Flowrate =     100.00; Fractions = ['0.0000', '0.0000', '1.0000']; Extra Info = None
    Stream = m3_out; Flowrate =         -F; Fractions = ['  x   ', '0.0000', '  x   ']; Extra Info = None
    Stream = m4_out; Flowrate =    -575.11; Fractions = ['0.0050', '0.9950', '0.0000']; Extra Info = None
    --------------------------------------------------
    END
# Check degrees of freedom again
extraction.degreesoffreedom()
# DOF analysis shows that extraction system is now solvable.
sol = extraction.solvesystem()
print(sol)
Output is:
    ==============================================================
    Process streams for SOLUTION TO LIQUID-LIQUID EXTRACTION are :
    ==============================================================
    Stream = m1_in ; Flowrate =     697.85; Fractions = ['0.1800', '0.8200', '0.0000']; Extra Info = None
    Stream = m2_in ; Flowrate =     100.00; Fractions = ['0.0000', '0.0000', '1.0000']; Extra Info = None
    Stream = m3_out; Flowrate =    -222.74; Fractions = ['0.5510', '0.0000', '0.4490']; Extra Info = None
    Stream = m4_out; Flowrate =    -575.11; Fractions = ['0.0050', '0.9950', '0.0000']; Extra Info = None
    --------------------------------------------------------------

# ALL FLOWRATES AND FRACTIONS ARE NOW KNOWN
# COMPUTE ACETIC ACID RECOVERY
# acetic acid in feed = m1_in * 0.18
aceticacid_infeed = overall_solution.m1_in.flowrate * overall_solution.m1_in.fractions[0]
# acetic acid in distillate =
aceticacid_indistillate = overall_solution.m5_out.flowrate * overall_solution.m5_out.fractions[0]
aceticacid_recovery = abs(aceticacid_indistillate/aceticacid_infeed *100)
print(f"Percent acetic acid from feed recovered in distillate = {aceticacid_recovery: 0.1f} %")
# Output is:
Percent acetic acid from feed recovered in distillate =  95.5 %

Example 21: Example `two unit process with extra info`¶

Example 21. A feed containing equimolar amounts of methanol (M) and water (W) is mixed with 10 moles of a 40 mol% aqueous methanol stream. The mixture enters a separation unit that creates two streams. A top stream exits that contains 70 mol% methanol and the rest water. The other stream, which is 70 moles, enters a second separation unit. A top stream exits the second unit as a 50% methanol /50% water mixture. The other stream is unknown in mole and methanol/water fractions. If the fresh feed to the system is 100 moles (the equimolar mixture) and the two top streams exiting the separation units have the same flow rate, find the molar flow rate and composition of the other stream exiting the second separation unit.

Youtube solution example 21

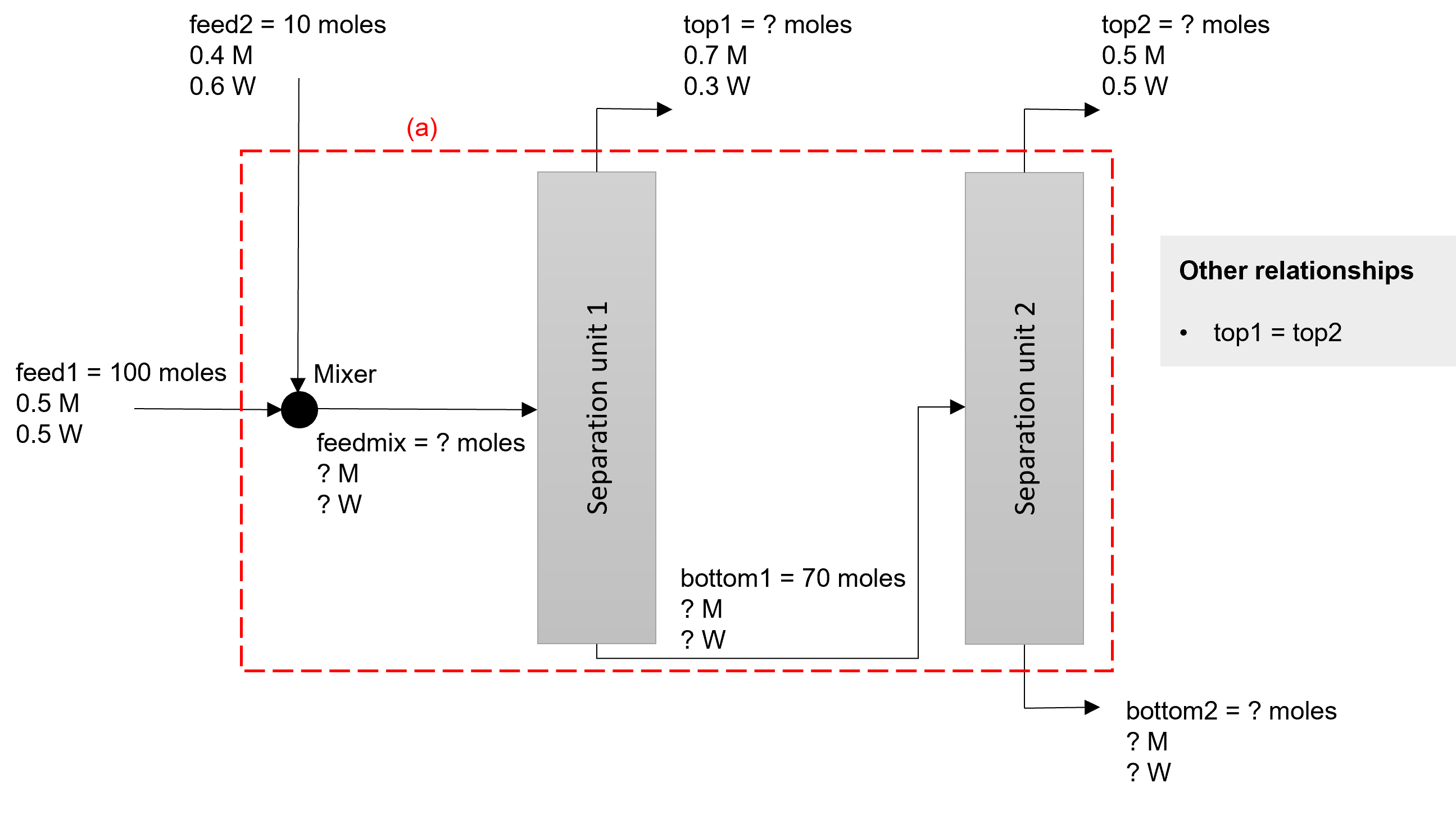
SOLUTION:

# EXAMPLE 20

from pychemengg.massbalances import physicalmassbalance as pmb

# Define the processes
overall = pmb.PhysicalProcess("overall")
mixer = pmb.PhysicalProcess("mixer")
unit1 = pmb.PhysicalProcess("unit1")
unit2 = pmb.PhysicalProcess("unit2")
# attach streams to mixer
streamnames = ["feed1", "feed2", "feedmix"]
flowrates = [100, 10, "-F"]
fractions = [[0.5, 0.5], [0.4, 0.6], ["x", "x"]]
mixer.feed1, mixer.feed2, mixer.feedmix = mixer.attachstreams(streamnames=streamnames, flowrates=flowrates, fractions=fractions)
# attach streams to unit 1
streamnames = ["unit1feed", "top1", "bottom1"]
flowrates = ["F", "-F", -70]
fractions = [ ["x", "x"], [0.7, 0.3], ["x", "x"]]
unit1.unit1feed, unit1.top1, unit1.bottom1 = unit1.attachstreams(streamnames=streamnames, flowrates=flowrates, fractions=fractions)
# attach streams to unit 2
streamnames = ["unit2feed", "top2", "bottom2"]
flowrates = [70, "-F", "-F"]
fractions = [ ["x", "x"], [0.5, 0.5], ["x", "x"]]
unit2.unit2feed, unit2.top2, unit2.bottom2 = unit2.attachstreams(streamnames=streamnames, flowrates=flowrates, fractions=fractions)
# attach streams to overall
streamnames = ["feed1", "feed2", "top1", "top2", "bottom2"]
overall.feed1, overall.feed2, overall.top1, overall.top2, overall.bottom2 = overall.attachstreams(streamnames=streamnames)
overall.feed1.setequalto(mixer.feed1, flowdirection="+")
overall.feed2.setequalto(mixer.feed2, flowdirection="+")
overall.top1.setequalto(unit1.top1, flowdirection="-")
overall.top2.setequalto(unit2.top2, flowdirection="-")
overall.bottom2.setequalto(unit2.bottom2, flowdirection="-")
overall.feed2.setextrainfo(["top1=1*top2"])

# print the systems to verify they have been correctly setup
print(mixer)
print(unit1)
print(unit2)
print(overall)
# Output not shown here to conserve space

# Compute degrees of freedom
mixer.degreesoffreedom()
unit1.degreesoffreedom()
unit2.degreesoffreedom()
overall.degreesoffreedom()

# Based on degrees of freedom analysis mixer can be solved
mixersol = mixer.solvesystem()
print(mixersol)
# Output is:
    ===========================================
    Process streams for SOLUTION TO MIXER are :
    ===========================================
    Stream = feed1  ; Flowrate =    100.00; Fractions = ['0.5000', '0.5000']; Extra Info = None
    Stream = feed2  ; Flowrate =     10.00; Fractions = ['0.4000', '0.6000']; Extra Info = None
    Stream = feedmix; Flowrate =   -110.00; Fractions = ['0.4909', '0.5091']; Extra Info = None
    -------------------------------------------
    END

# Use solution of "mixer" to update streams attached to other processes/systems.
unit1.unit1feed.setequalto(mixersol.feedmix, flowdirection="+")
# print unit 1 to verify it was updated
print(unit1)


#Find degrees of freedom again
unit1.degreesoffreedom()
unit2.degreesoffreedom()
overall.degreesoffreedom()
# DOF for unit1 = 0, therefore solve unit1
unit1sol = unit1.solvesystem()
print(unit1sol)
# Use solution of "unit1" to update streams attached to other processes/systems.
overall.top1.setequalto(unit1sol.top1, flowdirection="-")
unit2.unit2feed.setequalto(unit1sol.bottom1, flowdirection="+")
print (unit2)
print(overall)

#Find degrees of freedom again
unit2.degreesoffreedom()
overall.degreesoffreedom()
# DOF of overall = 0, therefore solve overall system
overallsol = overall.solvesystem()
print(overallsol)
# Output is:
    =============================================
    Process streams for SOLUTION TO OVERALL are :
    =============================================
    Stream = feed1  ; Flowrate =   100.00; Fractions = ['0.5000', '0.5000']; Extra Info = None
    Stream = feed2  ; Flowrate =    10.00; Fractions = ['0.4000', '0.6000']; Extra Info = ['top1=1*top2']
    Stream = top1   ; Flowrate =   -40.00; Fractions = ['0.7000', '0.3000']; Extra Info = None
    Stream = top2   ; Flowrate =   -40.00; Fractions = ['0.5000', '0.5000']; Extra Info = None
    Stream = bottom2; Flowrate =   -30.00; Fractions = ['0.2000', '0.8000']; Extra Info = None
    ---------------------------------------------
    END
# bottom2 stream provides the information sought in the problem.

Physical Process¶

Introduction¶

Examples¶

Example 1: How to define a physical process¶

Example 2: How to attach streams to a process¶

Example 3: How to name streams attached to a process¶

Example 4: How to print physical process and streams¶

Example 5: How to attach stream from one process to another process¶

Example 6: How to add or subtract streams¶

Example 7: How to perform degree of freedom analysis¶

Example 8: How to find unknown flow rate using overall balance¶

Example 9: How to find unknown fractions using fraction balance¶

Example 10: How to set extra information¶

Example 11: How to use perform_component_massbalance()¶

Example 12: How to find unknown flowrates and fractions¶

Example 13: How to use built in solvesystem()¶

Example 14: How to solve continuous process¶

Example 15: How to solve batch process¶

Example 16: How to solve multiple processes with extra info and recycle¶

Example 17: Example mixer with extra info¶

Example 18: Example distillation column - multiple feeds¶

Example 19: Example distillation column - extra info¶

Example 20: Example extraction-distillation with extra info¶

Example 21: Example two unit process with extra info¶

Example 1: How to `define a physical process`¶

Example 2: How to `attach streams to a process`¶

Example 3: How to `name streams attached to a process`¶

Example 4: How to `print physical process and streams`¶

Example 5: How to `attach stream from one process to another process`¶

Example 6: How to `add or subtract streams`¶

Example 7: How to `perform degree of freedom analysis`¶

Example 8: How to `find unknown flow rate using overall balance`¶

Example 9: How to `find unknown fractions using fraction balance`¶

Example 10: How to `set extra information`¶

Example 11: How to `use perform_component_massbalance()`¶

Example 12: How to `find unknown flowrates and fractions`¶

Example 13: How to `use built in solvesystem()`¶

Example 14: How to `solve continuous process`¶

Example 15: How to `solve batch process`¶

Example 16: How to `solve multiple processes with extra info and recycle`¶

Example 17: Example `mixer with extra info`¶

Example 18: Example `distillation column - multiple feeds`¶

Example 19: Example `distillation column - extra info`¶

Example 20: Example `extraction-distillation with extra info`¶

Example 21: Example `two unit process with extra info`¶